Polarisatsioon on üks antennide põhiomadusi. Kõigepealt peame mõistma tasapinnaliste lainete polarisatsiooni. Seejärel saame arutada antenni polarisatsiooni peamisi tüüpe.
lineaarne polarisatsioon
Hakkame mõistma tasapinnalise elektromagnetlaine polarisatsiooni.
Tasapinnalisel elektromagnetlainel (EM) on mitu omadust. Esiteks liigub energia ühes suunas (kahes ortogonaalses suunas väli ei muutu). Teiseks on elektriväli ja magnetväli teineteisega risti ja ortogonaalselt. Elektri- ja magnetväli on risti tasapinnalise laine levimissuunaga. Näiteks vaatleme võrrandiga (1) antud ühesageduslikku elektrivälja (E-välja). Elektromagnetväli liigub +z suunas. Elektriväli on suunatud +x suunas. Magnetväli on +y suunas.
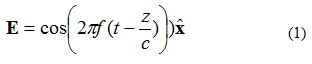
Võrrandis (1) jälgige tähistust: . See on ühikvektor (pikkuse vektor), mis näitab, et elektrivälja punkt asub x-suunas. Tasapinnaline laine on illustreeritud joonisel 1.
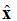
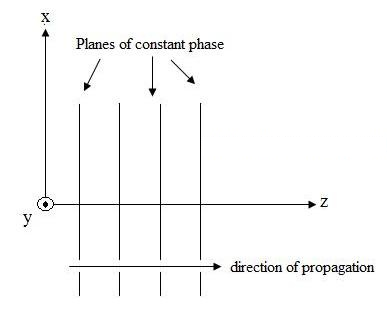
Joonis 1. +z-suunas liikuva elektrivälja graafiline esitus.
Polarisatsioon on elektrivälja jälje ja leviku kuju (kontuur). Näiteks vaatleme tasapinnalise elektrivälja võrrandit (1). Vaatleme aja funktsioonina asukohta, kus elektriväli on (X,Y,Z) = (0,0,0). Selle välja amplituud on kujutatud joonisel 2 mitmel ajahetkel. Väli võngub sagedusel "F".
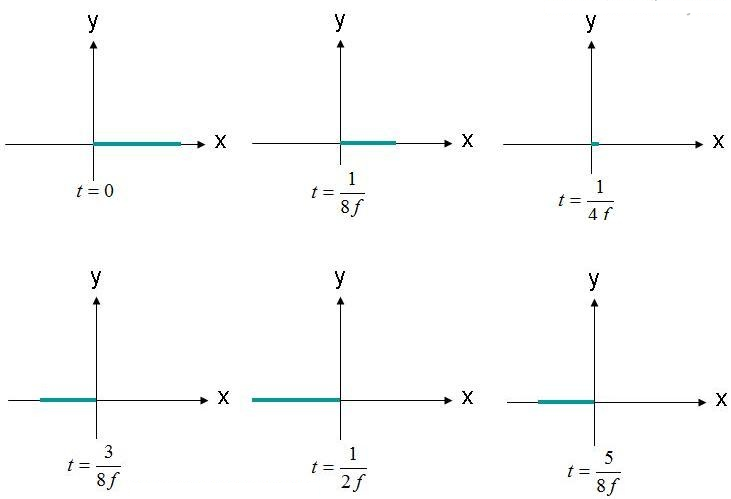
joonis 2. Vaatle elektrivälja (X, Y, Z) = (0,0,0) erinevatel aegadel.
Elektrivälja vaadeldakse alguspunktis, amplituudiga edasi-tagasi võngudes. Elektriväli on alati piki näidatud x-telge. Kuna elektriväli on suunatud piki ühte joont, võib öelda, et see on lineaarselt polariseeritud. Lisaks, kui X-telg on maapinnaga paralleelne, kirjeldatakse seda välja ka horisontaalselt polariseeritud. Kui väli on suunatud piki Y-telge, võib öelda, et laine on vertikaalselt polariseeritud.
Lineaarselt polariseeritud lained ei pea olema suunatud piki horisontaal- ega vertikaaltelge. Näiteks elektrivälja laine, mille piirang on suunatud piki joont, nagu on näidatud joonisel 3, oleks samuti lineaarselt polariseeritud.
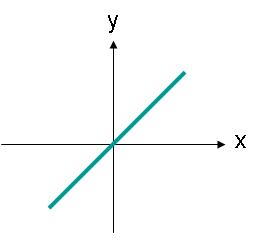
pilt 3. Lineaarselt polariseeritud laine elektrivälja amplituud, mille trajektoor on nurk.
Joonisel 3 kujutatud elektrivälja saab kirjeldada võrrandiga (2). Nüüd on elektriväljal x- ja y-komponent. Mõlemad komponendid on võrdse suurusega.
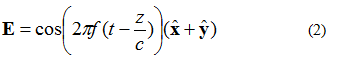
Üks asi, mida võrrandi (2) puhul tähele panna, on teise astme xy-komponent ja elektronväljad. See tähendab, et mõlemal komponendil on kogu aeg sama amplituud.
ümmargune polarisatsioon
Oletame nüüd, et tasapinnalise laine elektriväli on antud võrrandiga (3):
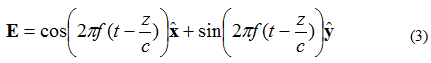
Sellisel juhul on X- ja Y-elemendid faasist 90 kraadi võrra nihkes. Kui välja vaadeldakse uuesti kujul (X, Y, Z) = (0,0,0), siis näeb elektrivälja ja aja kõver välja selline, nagu on näidatud allpool joonisel 4.
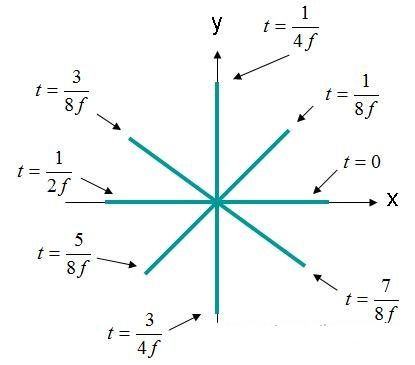
Joonis 4. Elektrivälja tugevus (X, Y, Z) = (0,0,0) EQ domeen. (3).
Joonisel 4 kujutatud elektriväli pöörleb ringis. Seda tüüpi välja kirjeldatakse ringpolariseeritud lainena. Ringpolarisatsiooni jaoks peavad olema täidetud järgmised kriteeriumid:
- Ümmarguse polarisatsiooni standard
- Elektriväljal peab olema kaks ortogonaalset (risti) komponenti.
- Elektrivälja ortogonaalsetel komponentidel peavad olema võrdsed amplituudid.
- Kvadratuurkomponendid peavad olema 90 kraadi faasist nihkes.
Lainekuju 4 ekraanil liikudes öeldakse, et välja pöörlemine on vastupäeva ja paremale suunatud ringpolarisatsiooniga (RHCP). Kui välja pööratakse päripäeva, on väli vasakukäeline ringpolarisatsioon (LHCP).
Elliptiline polarisatsioon
Kui elektriväljal on kaks risti asetsevat komponenti, mis on faasist 90 kraadi võrra nihkes, kuid on võrdse suurusega, on väli elliptiliselt polariseeritud. Arvestades tasapinnalise laine elektrivälja, mis liigub +z-suunas, mida kirjeldab võrrand (4):
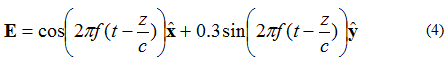
Elektrivälja vektori tipu asukoha asukoht on näidatud joonisel 5.
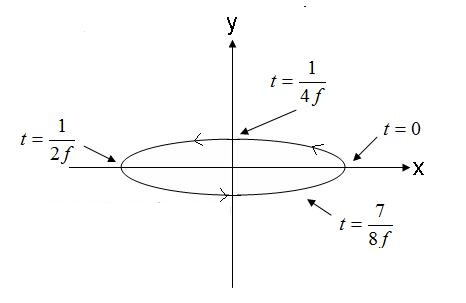
Joonis 5. Kiire elliptilise polarisatsioonilaine elektriväli. (4).
Joonisel 5 kujutatud väli, mis liigub vastupäeva, oleks ekraanist välja liikudes paremale elliptiline. Kui elektrivälja vektor pöörleb vastassuunas, on väli vasakule elliptiliselt polariseeritud.
Lisaks viitab elliptiline polarisatsioon selle ekstsentrilisusele. Ekstsentrilisuse ja põhi- ja kõrvaltelje amplituudi suhe. Näiteks laine ekstsentrilisus võrrandist (4) on 1/0,3 = 3,33. Elliptiliselt polariseeritud laineid kirjeldatakse täpsemalt põhitelje suuna abil. Lainevõrrandil (4) on telg, mis koosneb peamiselt x-teljest. Pange tähele, et põhitelg võib olla mis tahes tasanurga all. Nurk ei ole X-, Y- ega Z-telje sobitamiseks kohustuslik. Lõpuks on oluline märkida, et nii ring- kui ka lineaarne polarisatsioon on elliptilise polarisatsiooni erijuhud. 1,0 ekstsentriline elliptiliselt polariseeritud laine on ringpolariseeritud laine. Elliptiliselt polariseeritud lained lõpmatu ekstsentrilisusega. Lineaarselt polariseeritud lained.
Antenni polarisatsioon
Nüüd, kui oleme teadlikud polariseeritud tasapinnaliste lainete elektromagnetväljadest, on antenni polarisatsioon lihtsalt defineeritud.
Antenni polarisatsioon Antenni kaugvälja hindamine, tekkiva kiiratava välja polarisatsioon. Seetõttu liigitatakse antenne sageli "lineaarselt polariseeritud" või "paremakäeliste ringpolariseeritud antennidena".
See lihtne kontseptsioon on antenniühenduse jaoks oluline. Esiteks ei suhtle horisontaalselt polariseeritud antenn vertikaalselt polariseeritud antenniga. Vastastikkuse teoreemi tõttu edastab ja võtab antenn vastu täpselt samamoodi. Seetõttu edastavad ja võtavad vertikaalselt polariseeritud antennid vastu vertikaalselt polariseeritud välju. Seega, kui proovite edastada vertikaalselt polariseeritud horisontaalselt polariseeritud antenni, siis vastuvõttu ei toimu.
Üldjuhul kirjeldatakse kahe lineaarselt polariseeritud antenni puhul, mis on teineteise suhtes nurga ( ) võrra pööratud, polarisatsiooni mittevastavusest tingitud võimsuskadu polarisatsioonikao teguri (PLF) abil:
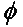
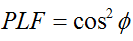
Seega, kui kahel antennil on sama polarisatsioon, on nende kiirgavate elektronväljade vaheline nurk null ja polarisatsiooni mittevastavuse tõttu ei teki võimsuskadu. Kui üks antenn on vertikaalselt ja teine horisontaalselt polariseeritud, on nurk 90 kraadi ja võimsust ei kanta üle.
MÄRKUS: Telefoni pea kohal erinevate nurkade all liigutamine selgitab, miks vastuvõtt mõnikord paraneb. Mobiiltelefonide antennid on tavaliselt lineaarselt polariseeritud, seega telefoni pööramine võib sageli sobitada telefoni polarisatsiooniga, parandades seeläbi vastuvõttu.
Ringpolarisatsioon on paljude antennide soovitav omadus. Mõlemad antennid on ringpolariseeritud ja ei kannata polarisatsiooni mittevastavusest tingitud signaali kadu. GPS-süsteemides kasutatavad antennid on parempoolse ringpolarisatsiooniga.
Oletame nüüd, et lineaarselt polariseeritud antenn võtab vastu ringpolariseeritud laineid. Samamoodi eeldame, et ringpolariseeritud antenn püüab vastu võtta lineaarselt polariseeritud laineid. Milline on sellest tulenev polarisatsiooni kadutegur?
Tuletame meelde, et ringpolarisatsioon on tegelikult kaks ortogonaalset lineaarselt polariseeritud lainet, mis on 90 kraadi faasist nihkes. Seega võtab lineaarselt polariseeritud (LP) antenn vastu ainult ringpolariseeritud (CP) laine faasikomponenti. Seega on LP-antenni polarisatsiooni mittevastavuse kadu 0,5 (-3 dB). See kehtib olenemata LP-antenni pööramise nurgast. Seega:
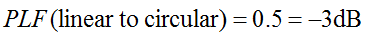
Polarisatsioonikao faktorit nimetatakse mõnikord polarisatsiooni efektiivsuseks, antenni mittevastavusfaktoriks või antenni vastuvõtufaktoriks. Kõik need nimetused viitavad samale kontseptsioonile.
Postituse aeg: 22. detsember 2023







